[Tutorial] Edge Centroid Decomposition – Another approach to divide and conquer on tree

Prerequisite

I assume that the readers are familliar with the standard centroid decomposition.

Let’s revisit centroid decomposition

Consider this classic problem – Given weighted tree with n <= 100000 vertices, count path with sum of edge weights equal to k. With Centroid decomposition, this essentially boils down to counting paths passing through the centroid whose length == k.

To do that, once we get the current centroid we can depth-first-search twice on each of centroid’s children subtree. The first depth-first-search add frequency of k - distance(centroid, u) to answer for each node u . The second depth-first-search put distance(centroid, u) into a std::set for each node u.

This way, we successfully count paths which have endpoints belonging to different subtrees of different centroid’s children. Careful! We also need to count paths which one of the endpoint is centroid itself.

map<int, int> freq;

DfsOne(u):
    answer := answer + freq[k - distance(cen, u)]
    For each children v of u:
        DfsOne(v)

DfsTwo(u):
    add one to freq[distance(cen, u)];
    For each children v of u:
        DfsTwo(v)

Solve(T):
    let cen be centroid of T

    freq.clear()

    freq[0] := 1

    For each children v of cen:
        DfsOne(v)
        DfsTwo(v)

    Delete the node cen and let T1, T2, ..., Tk be trees in the resulting forest.

    For each T' in T1, T2, ..., Tk:
        Solve(T')

Edge Centroid Decomposition

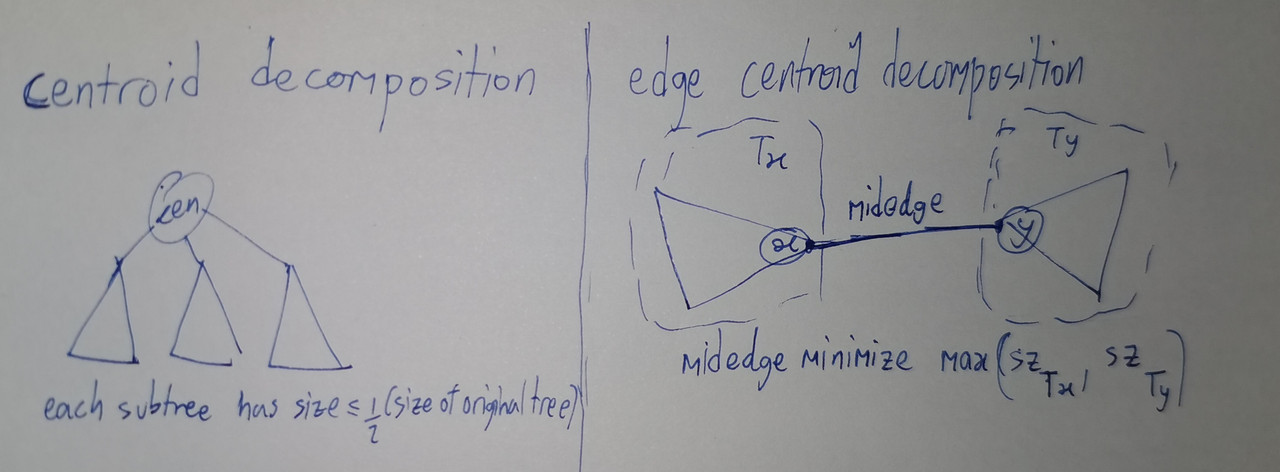
Instead of cutting vertices, we cut edges.

In standard centroid decomposition, we find vertex that, when removed, each resulting tree have size not exceeding half the size of original tree.

We can try something similar – finding an edge that, when removed, minimize the size of larger resulting tree (between the two).

image visualizing edge centroid decomposition

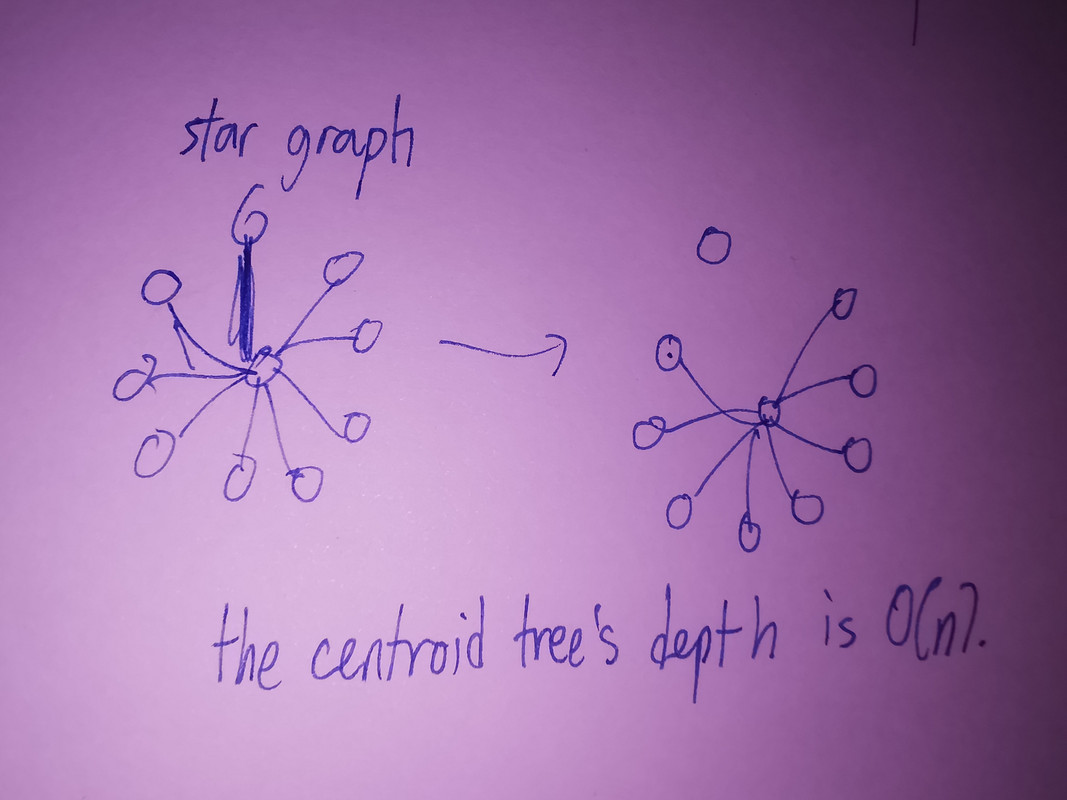
Bound on depth of centroid tree.

In standard centroid decomposition, since the tree size is halved in each layer, it it clear that depth of centroid tree <= log(n) / log(2).

However, in edge centroid decomposition, we cannot make such claims. Consider a star graph of order n, we can see that the tree size if reduced by merely one in each layer – doesn’t this make edge centroid decomposition useless?

image visualizing how star graph is a countercase

Binarizing the tree

If each node the tree has degree <= 3, it can be proven that there exists an edge (u, v) whose removal results in two trees, each with size not exceeding two-third of the original tree. [For details, look up ‘edge-weight tree-seperator lemma’]

Now, it is easy to see that on such a tree, the edge-centroid-decomposition will have depth bounded by log(n)/log(1.5), which is O(lg n)

So if we binarize the given tree , edge centroid decomposition can be used to solve the problem. [If you are not familiar with binarizing a tree, refers to the official solution of IOI2005_river]

Avoiding dynamic data structures

IOI11_race

As shown in the code above, we used a std::map (associative array) to store frequency of each distance. Since the edge centroid has only two endpoint x, y, we can put distances to vertices in x’s subtree into a sorted array, and binary-search on the array for all vertices in y’s subtree.

an implementation example of the problem (timus2085): https://ideone.com/3qlpeX

Another example

CF150E - freezing with style

This problem give a tree with weights on the edges, and askes for a simple path with maximal median.

First, we can binary-search-on-answer. To check if a simple path with median >= x exists, we can let the edge be -1 if original weight is less than x and +1 otherwise.

The problem is now reduced to finding a simple path with nonnegative sum of edge weights.

How to do so? At a first glance one might come up with an O(lg ^2 n) solution, one lg n from centroid-decomposition and another lg n from querying distances in a segment tree.

In edge centroid decomposition, let the edge centroid be (x, y), we can put distances from x to each node in its subtree in an array A[], and do so similarly for y in array B[]. (To avoid sorting, use BFS instead of DFS).

Now, we can utilize monotonic-queue trick on the two arrays, avoiding the lg n from segment tree.

implementation: https://codeforces.com/contest/150/submission/317153593

note: one can also remove one lg n from the the standard centroid decomposition, however it involves a more complicated method – sorting the subtrees by maximum depth

Practice problems

LuoguP3806 SpojQTREE4 SpojQTREE5